论文信息
题目:
Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks
会议:
KDD 2020
作者:

Introduction
摘要
多元时间序列建模一直是一个热门主题,吸引了来自不同领域的研究人员,包括经济、金融和交通。多元时间序列预测背后的一个基本假设是,其变量相互依赖,但仔细观察,可以说现有方法无法完全利用变量对之间的潜在空间依赖性。同时,近年来,图神经网络(GNN)在处理关系依赖方面表现出了很高的能力。GNN需要用于信息传播的定义明确的图结构,这意味着它们无法直接应用于事先不知道相关性的多元时间序列。在本文中,我们提出了一个专门为多元时间序列数据设计的通用图神经网络框架。我们的方法通过图形学习模块自动提取变量之间的单向关系,可以轻松地将诸如变量属性之类的外部知识整合到其中。进一步提出了一种新颖的混合跳跃传播层和一个扩张的起始层来捕获时间序列内的空间和时间依赖性。在端到端框架中共同学习图学习,图卷积和时间卷积模块。实验结果表明,我们提出的模型在4个基准数据集中的3个方面优于最新的基线方法,并在提供额外结构信息的两个交通数据集上与其他方法相比具有同等的性能。
时空图神经网络
图神经网络由于其置换不变性、局部连通性和组合性,在处理图数据方面取得了很大的成功。通过通过结构传播信息,图神经网络允许图中的每个节点都知道它的邻域。
多元时间序列预测可以很自然地从图的角度来看待。多元时间序列中的变量可以看作是图中的节点,它们通过隐藏的依赖关系相互连接。因此,利用图神经网络对多变量时间序列数据进行建模是一种很有前途的方法,可以在充分利用时间序列之间的相关性的同时,保留多变量时间序列的时间轨迹。
最适合用于多变量时间序列的图神经网络类型是时空图神经网络。时空图神经网络以多元时间序列和外部图结构作为输入,预测多元时间序列的未来值或标签。与不利用结构信息的方法相比,时空图神经网络已经取得了显著的改进。
挑战
**挑战1:未知的图形结构。**现有的GNN方法很大程度上依赖于预先设定的图结构来进行时间序列预测。在大多数情况下,多元时间序列没有明确的图结构。变量之间的关系必须从数据中发现,而不是作为基本真理知识提供。
**挑战2:图形学习与处理GNN学习。**虽然有图结构,但大多数GNN方法只关注消息传递(GNN学习),忽略了图结构不是最优的,需要在训练时进行更新。接下来的问题是如何在端到端框架中同时学习时间序列的图结构和GNN。
模型总结
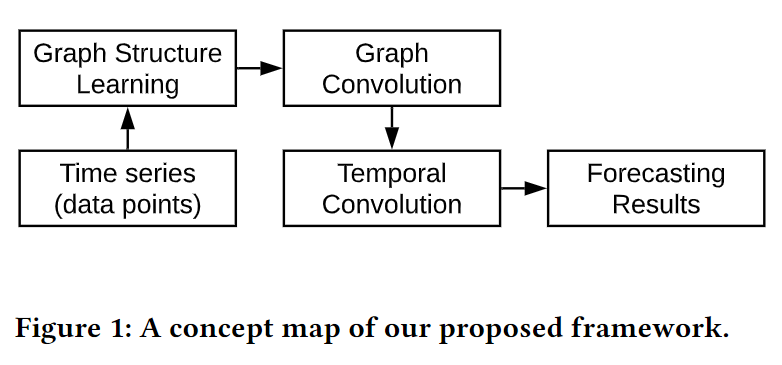
框架由三个核心组件组成:图学习层、图卷积模块和时序卷积模块。
- 针对挑战1,我们提出了一种新的图学习层,它基于数据自适应地表达稀疏图邻接矩阵。此外,我们开发了一个图卷积模块来解决变量之间的空间依赖性,给定由图学习层计算的邻接矩阵。
- 最后,我们提出了一个时间卷积模块,通过改进一维卷积来捕获时间模式。它既能发现多频率的时间模式,又能处理很长的序列。
- 由于所有参数都可以通过梯度下降来学习,因此提出的框架能够以端到端的方式对多元时间序列数据进行建模并同时学习内部图形结构
- 将时间序列划分成子组,适用于长短的时间序列任务
贡献
如图1所示,我们的框架由三个核心组件组成:图学习层、图卷积模块和时序卷积模块。
1.据我们所知,这是第一次使用图形神经网络从基于图形的角度对多变量时间序列数据进行研究。
2.我们提出了一个新的图学习模块来学习变量之间隐藏的空间依赖关系。该方法为GNN模型在处理数据时不需要明确的图结构打开了一扇新的大门。
3.我们提出了一个建模多元时间序列数据和学习图结构的联合框架。我们的框架比任何现有的时空图神经网络更通用,因为它可以处理多变量时间序列,无论是否使用预先修改过的图结构。
4.实验结果表明,我们的方法在4个基准数据集中的3个数据集上的性能优于现有的方法,并在两个提供额外结构信息的交通数据集上达到与其他GNNs相同的性能。
FRAMEWORK OF MTGNN
图2所示,最高级别的MTGNN由学习层,m个图卷积模块,m个时间卷积模块和输出模块组成。 为了发现节点之间的隐藏关联,图学习层计算图邻接矩阵,该矩阵随后用作所有图卷积模块的输入。图卷积模块与时间卷积模块交错,分别捕获空间和时间相关性。 为了避免梯度消失的问题,将残余连接从时间卷积模块的输入添加到图卷积模块的输出。 在每个时间卷积模块之后添加跳过连接。 为了获得最终输出,输出模块将隐藏特征投影到所需的输出尺寸。

时空卷积结合

红色是t时序卷积 蓝色是空间卷积
Graph Learning Layer
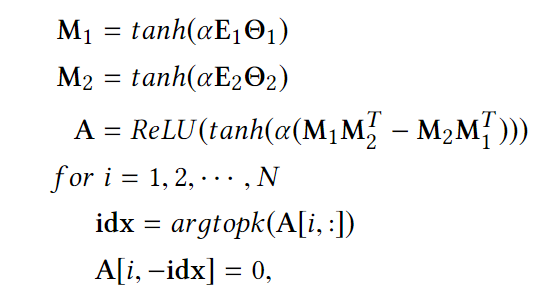
是随机的节点嵌入(可以进行预设。外部知识),是模型参数
Graph Convolution Module
图卷积模块旨在将节点的信息与邻居的信息融合在一起,以处理图中的空间依赖性。 图卷积模块由两个混合跃点传播层组成,以分别处理通过每个节点的流入和流出信息。 通过将两个混合跳跃传播层的输出相加获得净流入信息。 下图显示了图卷积模块和mix-hop传播层的体系结构
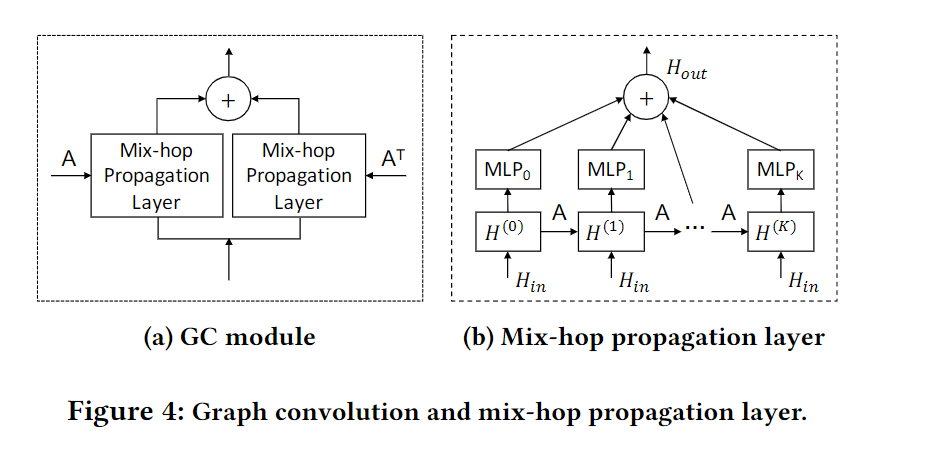
Mix-hop
给定一个图邻接矩阵,我们提出了混合跳跃传播层来处理信息流在空间上相关的节点。 所提出的混合跳跃传播层包括两个步骤-信息传播步骤和信息选择步骤。GC module 通过A和A的转置来整合双向的信息
信息传播:
信息选择:
k是传播的深度,表示上一层产生的输入隐状态,表示当前层的输出
信息传播通过k次卷积运算,计算了k-hop的邻居
信息选择则进行信息选择和整合
Temporal Convolution Module
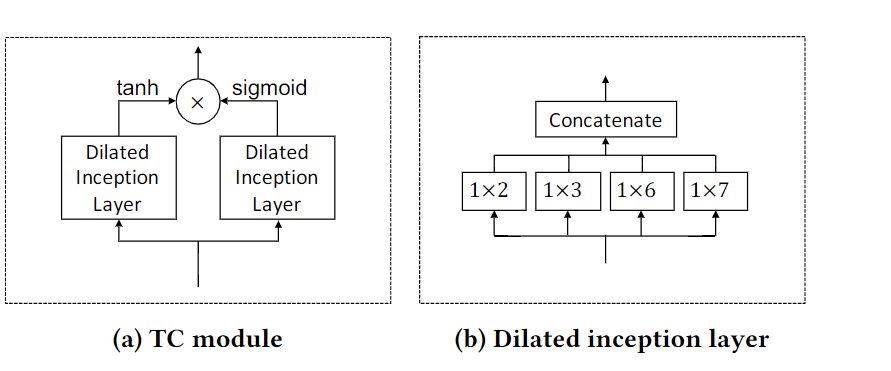
sigmoid起着门控的作用,控制信息流入
实验
数据集

多元时间序列的单步预测

多元时间序列的多步预测

消融实验
数据集:METR-LA

图学习方法对比